İnequalityconstrained optimization

COP is a CSP that includes an objective function to be optimized. Many algorithms are used to handle the optimization part. Constrained optimization with inequality constraints.

Week of the Course is devoted to identification of global extrema and constrained optimization with inequality constraints. This week students will grasp the concept of binding constraints and complementary slackness conditions. Moreover, the constraints that appear in these problems are typically nonlinear.

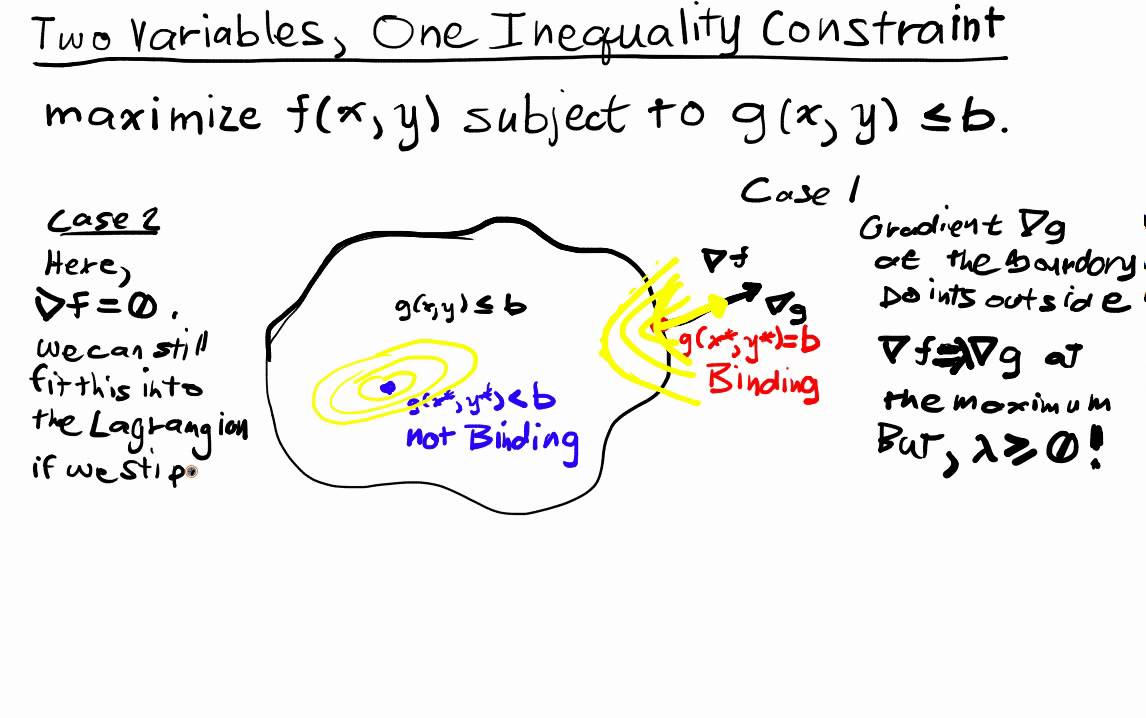
This motivates our interest in general nonlinearly constrained optimization theory and methods in this chapter. This video shows how to solve a constrained optimization problem with inequality constraints using the Lagrangian function.

In the above problem there are kinequality constraints and mequality constraints. This example shows how to solve an optimization problem containing nonlinear constraints. Include nonlinear constraints by writing a function that computes both equality and inequality constraint values. If, then (as in general ), indicating is not an extremum without the constraint, i. This is an inequality constrained optimization.

In general, we might write these problems like this. So minimize it over the values of x that satisfy these two constraints.

Consumers make decisions on what to buy constrained by the fact that their choice must be affordable. Firms make production decisions to maximize their profits subject to the constraint that they have limited production capacity. A line search filter SQP method for inequality constrained optimization is presented.

This method makes use of a backtracking line search procedure to generate step size and the efficiency of the filter technique to determine step acceptance. At each iteration, the subproblem is always consistent, and it only needs to solve one QP subproblem. A generalized gradient projection filter algorithm for inequality constrained optimization is presented.

It has three merits. These are easier to solve than the original inequality-constrained problem Equation 33. To solve the approximate problem, the algorithm uses one of two main types of steps at. The third is that the.

In this paper, by means of the concept of the working set, which is an estimate of the active set, we propose a feasible sequential linear equation algorithm for solving inequality constrained optimization problems. An inequality-constrained linear optimization problem in two variables.

Ask Question Asked years, months ago. Active years, months ago. Once I got through the text-to.

In solving a constrained optimization problem, such as the OPF, there are two general classes of constraints, equality and inequality. Equality constraints are constraints that always have to be enforced. That is, they are always "binding".

In the most general case, both the objective function and the constraints are represented as Tensor s, giving users the maximum amount of flexibility in specifying their optimization problems. We propose a new algorithm for the nonlinear inequality constrained minimization problem, and prove that it generates a sequence converging to points satisfying the KKT second order necessary conditions for optimality. This shows that the method is not very sensitive to the value of provided 10.

Conclusions We have proposed a new algorithm to solve functional inequality constrained optimization problems, where the functional constraints are transformed and treated as a penalty function. References Bertsekas, D. When iteratively solving optimization problems arising from engineering design applications, it is sometimes crucial that all iterates satisfy a given set of “hard” inequality constraints, and gene.

TFCO is a library for optimizing inequality-constrained problems in TensorFlow 1. As we know, Lagrange multiplier method is one of the efficient methods to solve problem (NLP). We also show how inequality constrained splines can be used to produce good or optimal knots, and we describe applications to parametric curves and surfaces in CAGD.

In this paper, we propose a new penalty-free method for solving nonlinear equality constrained optimization. This method uses different trust regions to cope with the nonlinearity of the objective function and the constraints instead of using a penalty function or a filter.